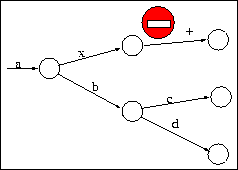
 R1. The pruning process does not apply
to transitions belonging to annotations (the annotations are separated
from the inflected forms by the annotation separator - represented
here by ``+'').
R1. The pruning process does not apply
to transitions belonging to annotations (the annotations are separated
from the inflected forms by the annotation separator - represented
here by ``+'').
All strings constructed in the way described in section 3.3 are used to build a finite state automaton. As the strings consist of inverted inflected forms, followed by an annotation separator, and by annotations, the resulting automaton can already be used to the annotations from the corresponding inflected form. The inflected form that is to be analyzed should be inverted, and one should look for the resulting string in the automaton. If the word is not in the lexicon, the search fails at a certain state, i.e. no transition labeled with the next letter of the string can be found. In such case, all annotations that can be reached from that state should be printed. Although the automaton could be used for our purposes, it is unnecessarily big, as it contains much useless information.
As word endings normally decide what annotation should be associated with a given word, the automaton has a particular structure. For a given word, the first few states have many outgoing transitions. Then, there is a chain of states linked with each other with single transitions. Passing to annotations, a more complicated transition network appearers again. As for any state in the central part, there is only one way leading from the state to the appropriate annotations, it represents no useful information for our purpose. So all states from that part can be pruned, along with the corresponding transitions.
Pruning is governed by the following rules:
 R1. The pruning process does not apply
to transitions belonging to annotations (the annotations are separated
from the inflected forms by the annotation separator - represented
here by ``+'').
R1. The pruning process does not apply
to transitions belonging to annotations (the annotations are separated
from the inflected forms by the annotation separator - represented
here by ``+'').
This rule should be obvious, because annotations are what we want to
obtain in the recognition phase. The transitions that are pruned
belong to the inflected forms, and more precisely: to their beginnings
that do not influence the annotations.
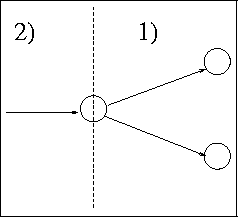 R2. A transition can be removed only if the pruning process has
already visited all transitions that can be reached through the
target state, except the transitions representing annotations. In
other words, the states are visited (and the outgoing transitions
pruned if possible) in the postorder method.
R2. A transition can be removed only if the pruning process has
already visited all transitions that can be reached through the
target state, except the transitions representing annotations. In
other words, the states are visited (and the outgoing transitions
pruned if possible) in the postorder method.
This means that we traverse the automaton recursively in depth, cutting
unneeded transitions on the way back.
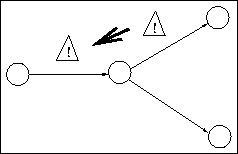 R3. A transition cannot be removed if the target state has a
transition that does not belong to annotations, but cannot be
removed. The warning sign above a transition in the figure shows
that the transitions cannot be removed. We use a different sign than
in R1, as the reason the transition cannot be removed is different.
R3. A transition cannot be removed if the target state has a
transition that does not belong to annotations, but cannot be
removed. The warning sign above a transition in the figure shows
that the transitions cannot be removed. We use a different sign than
in R1, as the reason the transition cannot be removed is different.
This means that the target state has transitions that distinguish
between different annotations, i.e. they lead to different sets of
annotations. We do not want to lose that distinction.
 R4. A state can always be replaced with an equivalent one (i.e. a
state with the same transitions leading to the same states).
R4. A state can always be replaced with an equivalent one (i.e. a
state with the same transitions leading to the same states).
The automaton should be kept minimal .
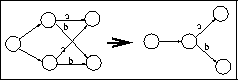
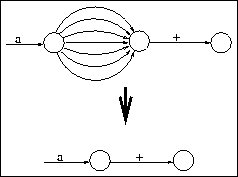 R5. A state with all transitions leading to one state can be removed
with all transitions, and transitions that point to it should be
replaced by transitions pointing to the target state.
R5. A state with all transitions leading to one state can be removed
with all transitions, and transitions that point to it should be
replaced by transitions pointing to the target state.
This is the rule that actually cuts transitions. Note that it also applies to states with one only transition.
The consequence of the rules R2 and R5 is that we cannot remove states (and transitions that lead to them) if they have transitions leading to different sets of annotations. This is because the rule R2 ensures that all transitions of a visited state lead to states that either cannot be removed, or that have an outgoing transition labeled with the annotation separator.