The taxonomy presented in fig. 4.1 is from [Wat93a], with an additional branch for deterministic acyclic automata. Bruce Watson prepares a new, extended taxonomy, containing more algorithms than those shown here.
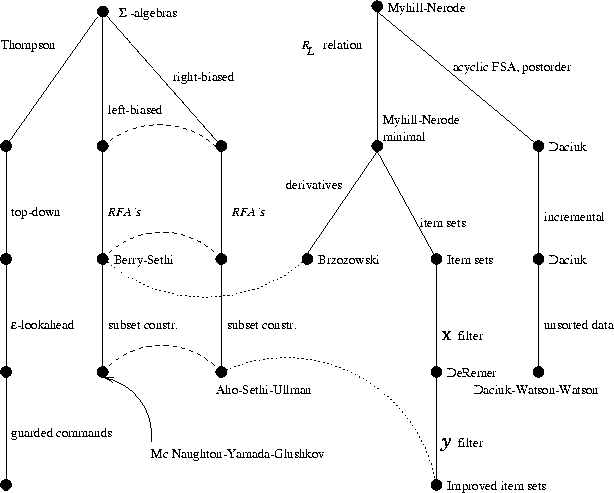
Figure 4.1: The family trees of finite automata
constructions taken from [Wat93a] with
modifications. Solid edges denote refinements of the solution
(and therefore explicit relationships between
constructions). They are labeled with the name of the
refinement
The figure shows two families of construction
algorithms. 
-algebras are a generalization of regular
expressions. The algorithms constructing finite-state automata using
regular expression date from the early days of computer science.
The same results can be obtained in a variety of ways, as the
diagram shows. Another family of methods is based on the Myhill-Nerode
theorem (or at least the methods that belong to it can be derived from
that theorem). Incremental algorithms for acyclic automata are added
as a separate branch in the Myhill-Nerode tree. In the diagram, the
algorithm for data in arbitrary order is derived from the algorithm for sorted
data. This is in line with the development of those algorithms by the
author. Note that the passage through the sorted data algorithm is not
necessary to arrive at the version for data in arbitrary order; actually,
Richard Watson and Bruce Watson developed the same algorithm without
considering the version for sorted data.