A finite-state automaton is a device that can be in one of a finite
number of states . In certain conditions, it can switch to
another state. This is called a transition .
When the automaton starts working (when it is switched on), it can be
in one of its initial states. There is also another important subset
of states of the automaton: the final states. If the automaton is in a
final state when it stops working, it is said to accept its
input. The input is a sequence of symbols. The interpretation of the
symbols depends on the application; they usually represent events, or
can be interpreted as ``the event that a particular data became
available''. The symbols must come from a finite set of symbols,
called the alphabet . If a particular symbol in a
particular state triggers a transition from that state to another one,
that transition is labeled with that symbol. The labels of
transitions can contain one particular symbol that is not in the
alphabet. A transition is labeled with 
(not present in the
alphabet) if it can be traversed with no input symbol.
It is convenient to present automata as directed graphs. The vertices denote states. They are portrayed as small circles. The transitions form the edges - arcs with arrows pointing from the source state (the state where the transition originates) to the target state. They are labeled with symbols. Unless it is clear from the context, the initial states have short arrows that point to them from ``nowhere''. The final states are represented as two concentric circles.
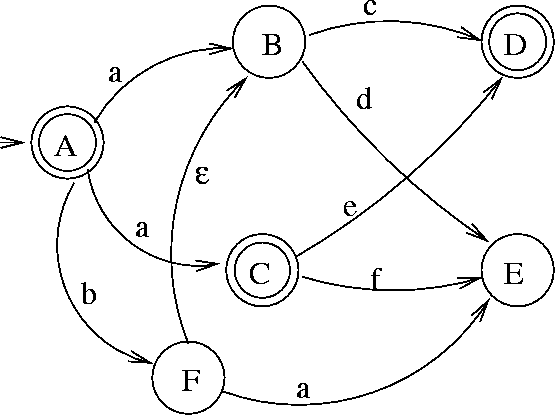
Figure 2.1: Sample finite-state automaton
The example automaton (fig. 2.1) contains 6 states labeled A, B, C, D, E and F. The state labeled A is initial. The states A, C, and D are final. The automaton contains no cycles, as it is impossible to leave a state, follow some transitions, and return in this way to the same original state.
Starting in one of the initial states, the automaton processes a
sequence of input symbols. In a given state, it checks if the next
input symbol matches any of the labels of the transitions that go out
of the state. If so, the automaton follows it to the target state of
the transition. If is among the labels, the transition it
labels is followed without reading the input. There may be more than
one transition with the same label, or a transition with a matching
label and a transition labeled with . In that case, the
decision which path to choose is arbitrary. If there is no transition
that matches the input symbol (in particular, if there is no
-transition), the automaton stops and rejects the input. The
input is accepted when all input is read and matched by transitions
and the automaton is in a final state.
A set of sequences of symbols gathered by pursuing all paths from
initial states to the final ones is called the
language
accepted by the
automaton. E.g. the example automaton (fig. 2.1)
accepts the language 
. The symbol
, meaning an empty input, is accepted because the initial
state A is also the final one. a is accepted, because
there is a transition from A to C labeled with a,
and C is a final state. The input bc is accepted,
because the control in the automaton can go from A to F on
a, and then it can follow the -labeled transition to
B, and then a transition labeled c to D, which is a
final state. The sequences: {ad, ae, af, ba} are all rejected,
because E is not a final state. The language of the automaton
in fig. 2.1 is finite, because the automaton
contains no cycles.
An automaton that has no -labeled transitions is called
-free. An automaton that has one initial state, is
-free, and for each state there is at most one transition
labeled with the same symbol is called a deterministic finite-state
automaton .
The automaton from fig. 2.1 can be transformed into
the deterministic automaton from fig. 2.2.
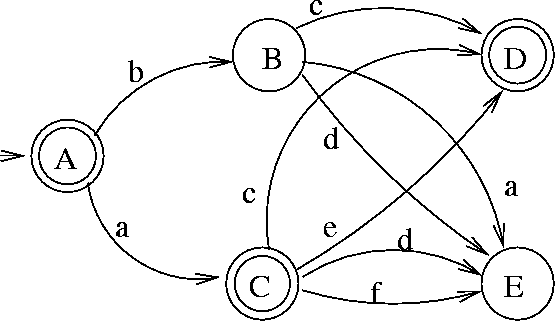
Figure 2.2: Deterministic version of the sample automaton
A state is said to be reachable from another state iff there is a sequence of transitions leading to the state from that other state. An automaton is said to be start-useful iff every state is reachable from any of its initial states. An automaton is useful iff it is start-useful and for every state there is at least one final state reachable from that state. The automaton from the fig. 2.2 is not useful; its useful version is presented in fig. 2.3. That version accepts the same language.
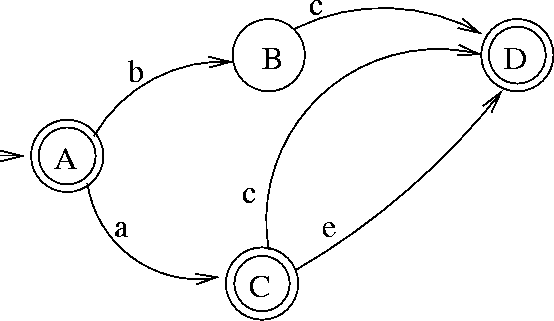
Figure 2.3: Useful version of the sample deterministic automaton
An automaton is said to be acyclic when it contains no cycles, i.e. it is not possible to arrive at the same state twice when following the transitions. All automata in figures presented in this dissertation are acyclic.
Formally, an automaton is a 5-tuple 
, where Q is a set of states, 
is a set of initial (or starting)
states, 
is a set of final states, 
is the
alphabet , and 
is a partial mapping 
denoting transitions. We extend the mapping to 
. The size of the
automaton, |M|, is equal to the number of states |Q|. We define
the language
accepted by the automaton M to be:
Let the mapping 
be the right
language of a state
q in M (the set of all strings over 
that will take one
from state q to any final state of M using the extended transition
relation 
):
The consequence of the Myhill-Nerode theorem ([HU79]) is that among many automata that accept a given language there is one (up to isomorphism) that has a minimal number of states. It is called a minimal automaton . The automaton in fig. 2.3 is minimal.
The property of minimality of is defined as follows ([Wat93a], [Wat93b], [Wat95]):
We will use, however, an alternative definition of
minimality of
([Wat93a],
[Wat93b]):
is a
property specifying that all states can be reached from the start
state, and it is defined as follows:
Of particular interest for the NLP community are deterministic acyclic
finite state automata (DAFSA)
, because they are best suited for
representing dictionaries (of various sorts). Whenever we refer to an
automaton (or FSA) throughout this paper, we mean an acyclic, deterministic
finite state automaton (DAFSA), unless explicitly stated otherwise. Several
definitions given above can be rewritten in a simpler way: a
deterministic, finite-state automaton is a 5-tuple
, where Q is a set of states, 
is the starting state, is a set of final states,
is the alphabet , and is a partial
mapping 
denoting
transitions. We extend the mapping to 
as in [HU79]. The
definitions of the language accepted by an automaton, the right
language of a state, and of the 
property for DAFSA
become simpler:
It is possible to use alternative definition of an FSA: 
, where the meaning of Q, , i, and F is
the same as above, and E is a relation 
-
an alternative expression of the function from above. This
alternative definition may be more useful in descriptions below.
The algorithms described in this paper operate on classical
DAFSA (deterministic acyclic finite-state automata). However, our
implementation uses a different kind of automata:
finite-state automata with final transitions (FSA-FT)
.
We define such automaton as , where Q is the
finite set of states, is the alphabet , 
is the set of the initial states of the automaton, 
is a set of transitions, and 
is the set of final transitions. We say that the FSA-FT accepts a word
if for each symbol from the input a transition was found, and the last
transition it traversed while recognizing the word was final.
We define a transformation of a classical finite-state
automaton into a finite-state automaton with final transitions: for every
FSA we find an FSA-FT 
,
where 
, i' is the new initial state, 
, and 
.
Let 
to be the transitive closure of F defined by the
following recursive relation:
then 
then 
Now we can define the language of the FSA-FT to be:
For every deterministic acyclic finite-state automaton 
that does not accept empty input (written as ),
i.e. 
, or 
, we can find a deterministic acyclic finite-state automaton with
final transitions (DAFSA-FT) 
,
, where . We will call this transformation moving
markers . It preserves the number of states and
the number of transitions. Because such a transformation exists, and
it is defined for the minimal
automata , we can write that
.
Minimal deterministic acyclic finite-state automata with final transitions can indeed be smaller than their classical counterparts (see fig. 2.4). The definition of minimality for an FSA-FT is the same as for the classical FSA, but the definition of the right language of a state in FSA-FT must change:
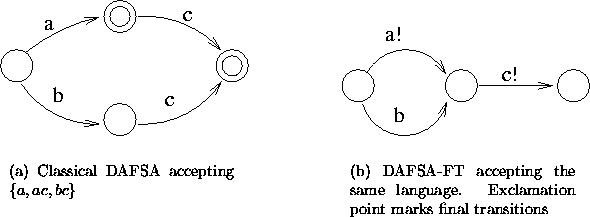
Figure 2.4: Classical minimal deterministic acyclic FSA and the
corresponding FSA with final transitions
Note that for DAFSA-FT 
. This is different from the
classical automata, where 
. That difference is very
important. It means that the recognition of a word is moved from a
final state in the classical automaton to the transition reaching
that state in the FSA-FT, resulting in the removal of the empty
string () from the right language of that automaton. Let be a DAFSA (a classical one), and 
be a DAFSA-FT obtained by the transformation
moving markers . We can write:
If we can find two states in the classical FSA that have the same right languages except for the empty string, we can merge the states together in a deterministic acyclic finite-state automaton with final transitions. This makes the resulting automaton smaller, i.e. it has less states and less transitions than the corresponding classical finite-state automaton.
Note that as most implementations of automata have implicit states (only transitions are represented explicitly), this new kind of automata saves space at no cost.
The automata with final transitions can be seen as Mealy's automata where the property of being final is the output label. Therefore, they can be perceived more as a notational convention than a new kind of automata. However in transducers, that property would have to be concatenated with the output labels.
