Transducers are automata that have transitions labeled with two symbols. One of the symbols represents input, the other - output. Transducers translate (or transduce) strings. In automata theory (see [HU79]) they are called Mealy's automata.
Transducers can be seen as automata with transitions labeled with
symbols from 
, where 
and 
are the alphabets of input and output,
respectively. With such a perception in mind, all the definitions for
automata hold for transducers. The alphabets and
are frequently the same, so the definition ([RS95])
becomes simply 
, where 
is a finite
alphabet, Q is a finite set of states or vertices, 
is the
initial state, 
is the set of final states, and 
is the set of transitions or edges. The state transition function
d that maps 
into 
is defined as 
. The emission
function 
maps 
into 
, and is defined as
.
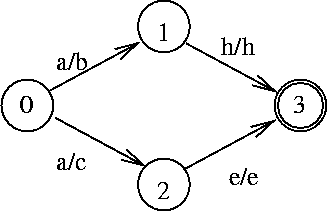
Figure 2.5: Simple transducer (adopted from [RS95])
Figure 2.5 shows a transducer T=({a,b,c,e,h}, {0,1,2,3}, 0, {3}, {(0,a,b,1), (0,a,c,2), (1,h,h,3), (2,e,e,3)}). It translates ab to bh and ae to ce.
Transducers translate or transduce strings. A transducer T is said
to represent the transducing mapping f from 
to
. Let 
be the transitive closure of E defined by
the following recursive relation ([RS95]):
than 
then 
. One writes f = |T|. In the example figure,
|T|(ah)=bh and |T|(ae)=ce. If, for some input w, more than one
output is allowed, then f is called a rational
transduction . Otherwise it is called a
rational function .
Because transducers are used as a device to compute a function (or to
translate one string into another), a different definition of being
deterministic is used. In that definition, a transducer is said to be
deterministic iff both the transition function d and the emission
function lead to sets containing at most one element. More
formally, 
. Traditionally, such
deterministic transducers are called
subsequential (sequential
transducers
are deterministic transducers for which all states are final). For
subsequential transducers, the transducing function can be computed by
deterministically following a single path in the transducer.
The transducer in figure 2.5 is not subsequential;
it computes a rational function. Because both transitions leaving
the first state have a as their input labels, 
one cannot determine which path to follow without looking at further
input.
Subsequential transducers are defined as seven-tuples
, where the meaning of , Q,
i, and F is the same as in simple transducers described above,
is the deterministic state transition function that maps 
on Q, * is the deterministic emission function that
maps on (this function should not be
confused with the Kleene's star, which is written as a superscript),
and the final emission function 
maps F on . One
writes 
, q * a = w' and 
. Figure 2.6 shows a subsequential transducer
that accepts the same language as the transducer from
fig. 2.5.
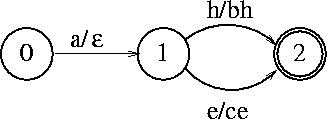
Figure: Subsequential transducer - a transformation of the
transducer from fig. 2.5 (taken from
[RS95])
Subsequential transducers are faster in recognition tasks, but may take more space. They are faster, because one always follows a single path in the automaton, and there is no need to go back, as it is the case with simple transducers. They may take more space as one needs to store strings instead of characters (symbols) in transitions.