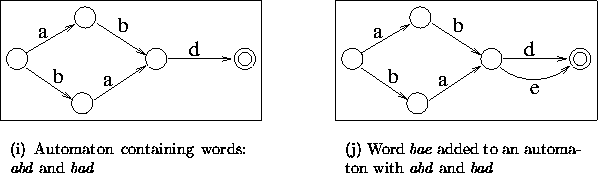
Figure 4.6: The result of adding the word bae to a minimized automaton containing abd and bad. The automaton inadvertently contains abe as well.
Sometimes it is difficult or impossible to sort the input data before construction of an automaton (for example, there is not enough disk space to store and sort data or the data comes from another program or physical source. An incremental automaton building algorithm may still be very useful in those situations, although unsorted data makes it more difficult to merge the trie building process, and the minimization process . There are two extreme solutions:

Figure 4.6: The result of adding the word bae to a minimized automaton
containing abd and bad. The automaton inadvertently contains
abe as well.
The description of the second case is included here. Every time a word is added to the automaton, it is minimized . This could lead to modifications of the parts of the automaton that had previously been minimized. Similar to the algorithm for sorted data, when a new word is added, the common prefix is searched for in the automaton. However, one cannot assume that the path containing the prefix will not be changed. If there are states in the path traversed by the word in the pre-existing automaton that are targets of more than one incoming transition (known as confluence states , then appending another transition to the last state in the path would accidentally add more words than desired (see fig. 4.6).
To avoid generation of such spurious words, all states in the common prefix from the first state that has more than one incoming transition must be cloned. Cloning is the process of creating a new state which has outgoing transitions with the same labels and to the same destination states as a given state. If we compare the minimal automaton to an equivalent trie, we note that a confluence state can be seen as a root of several original isomorphic subtrees merged into one (as described in the previous section). One of the isomorphisms needs to be modified, so it must be separated from the others by cloning its root. The rest of the word must be appended. The new subtree is then modified, so its states must be removed from the register, and either re-registered, or replaced by another (equivalent) state already in the register. If there are no confluent states in the common prefix (up to a confluence state), then adding the rest of the word does not differ from the algorithm for sorted data.
When the process of traversing the common prefix (up to a confluence state) and adding the suffix is complete, the modifications are not over. The previous states in the prefix path may need to be changed, because the right languages of those states may have changed. We must recalculate the equivalence relation for all states on the path of the new word. The process could actually make the new minimal automaton smaller. The resulting algorithm is shown in fig. 4.7.

Figure 4.7: Incremental construction algorithm from data in arbitrary order
The replace_or_register procedure from the previous algorithm
needs to be modified slightly. As new words are added in arbitrary
order, and one can no longer assume that the last child is the one
that has been added or modified last. Now, all children of a state
must be checked, not only the most recently altered child. However,
only one child may need treatment, so the execution time is of the
same order. In the previous algorithm, add_suffix is never
passed ![]() as an argument. In this version, it may happen. The
effect is that the current state should be marked as final since the
common prefix is already the entire word.
as an argument. In this version, it may happen. The
effect is that the current state should be marked as final since the
common prefix is already the entire word.
As before, the main loop executes m times, where m is the
number of words accepted by the automaton. The inner loops are
executed at most |w| times for each word. Putting a state into the
register is ![]() , and it may be constant for regular
data when using a hash table. The same estimation is valid for a
removal from the register. So the time complexity of the algorithm
remains the same, but the constant changes. For sorted data, only a
small part of the automaton is changed each time a new word is
added. For the data in arbitrary order, the changes frequently
percolate all the way back to the start state, so processing each word
costs more.
, and it may be constant for regular
data when using a hash table. The same estimation is valid for a
removal from the register. So the time complexity of the algorithm
remains the same, but the constant changes. For sorted data, only a
small part of the automaton is changed each time a new word is
added. For the data in arbitrary order, the changes frequently
percolate all the way back to the start state, so processing each word
costs more.
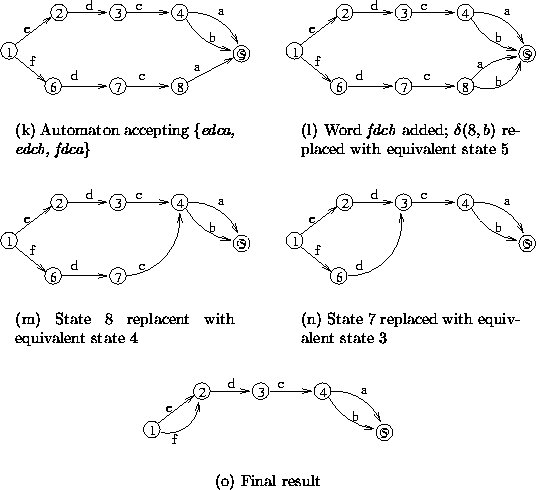
Figure 4.8: Examples of Construction process from unsorted data:
changes propagate to the root
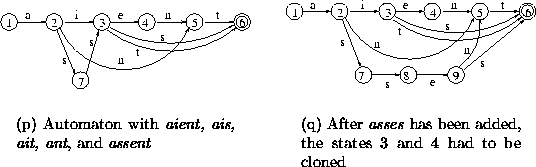
Figure 4.9: Examples of construction process from unsorted data: cloning