Hashing maps keywords from a
given set of n keywords into numbers (addresses). If the mapping is
a bijection into a set ![]() (or
(or ![]() ), the hashing
is said to be ``perfect''.
), the hashing
is said to be ``perfect''.
Perfect hashing can be implemented in form of an automaton ([Roc95]). We treat the keywords as words of the language accepted by an automaton. Therefore, we can build an automaton that accepts that language, and consequently, stores all those words. Because the language contains a finite number of words, the automaton must be acyclic. To be efficient, it must be deterministic.
We need to establish a mapping between words and their cardinal numbers. Note that if all transitions in an automaton are sorted by their labels, such mapping implicitly exists in the automaton. Words are ordered by the order of their appearance in the automaton when traversed using the postorder method. So the mapping can be provided by counting all words that precede the given word in the automaton.
Counting words can mean traversing the whole automaton, so it is computationally impractical. However, it is possible to precompute some values so that the search be effective. Let us look again at another sample automaton (deterministic version) at fig.6.8.
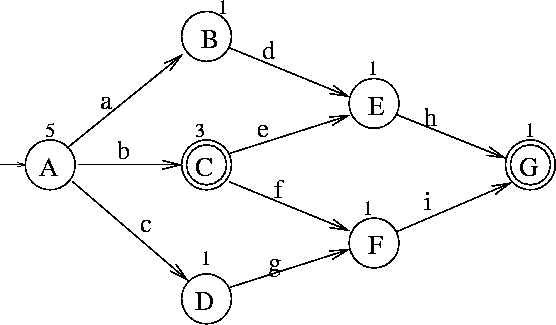
Figure 6.8: Sample deterministic finite-state automaton implementing
perfect hashing
Small numbers near state circles tell how many words (suffixes of the words accepted by the automaton) are accepted by the part of the automaton that is reachable from that state, that state including. Formally, that number can be computed as:
![]()
That number can be calculated recursively using dynamic programming:
![]()
These numbers can be precomputed and stored at their respective states, so that they be available during dictionary lookup.
To find the number associated with a given word, we find that word in the automaton, doing some calculations at states that we pass by. What we are looking for is the number of words that precede the given word in the automaton. E.g. the word bfi is the fourth word recognized by the automaton from fig. 6.8. To find that it is indeed the fourth word, we first look at the start state - A. As we must go through that state, its count does not count (it is the total number of words of the language accepted by the automaton). We see that b is the label of the second transition. The first transition leads to a state that has its count value set to 1. this means that there is one word in the automaton that precedes all words that start with b. We add it to the total, which is initially zero. The transition labeled b leads us to the state labeled with C. This state is final, so because shorter words come before longer ones, we must add 1 to the total when we go through. We add another 1 as well, because f is the second transition in that state, and the first transition leads to a state that has count value set to 1. Now the total is 3. With f, we go to F, which is not final, so there is nothing to add to the total, and then we go to G. G is a final state, so bfi is accepted. The total is 3, meaning there are 3 words before bfi in the automaton, so bfi is the fourth.