The algorithms presented here are new and original. They have been developed during the author's stay at ISSCO, Geneva, Switzerland. At the same time, and independently, those algorithms were also developed by Bruce Watson and Richard Watson.
By exploiting particular features of deterministic acyclic FSA as opposed to finite-state automata in general, it was possible to devise a way to build automata more efficiently than it was possible in general case.
An algorithm described in [Rev91] also constructs an automaton from sorted data while performing a sort of minimization on-the-fly. Data is sorted in reverse order, and that property is used to compress the endings of words while building the automaton. This is called a pseudo-minimization , and it must be supplemented by a true minimization afterwards. Although that technique is more economic in its use of memory than standard techniques, we are still left with an automaton that is not minimal in an intermediate state. Revuz writes that for the DELAF dictionary, the automaton after the pseudo-minimization phase was 8 times bigger than the minimal one. Our algorithms need the space for the minimal automaton, and the register. The size of the register is proportional to the number of states in the automaton, and it may have index structures proportional to the logarithm of the number of states. In any case, its size is much smaller than the size of the automaton.
Compared to Revuz'es algorithm, our algorithms use less memory, because they minimize the automaton each time a new word has been added. Our algorithm for sorted data makes it possible to perform some modifications that possibly reduce its size on-the-fly (such as e.g. pruning required for building a morphological guesser) because minimized parts of the automaton are left unchanged till the end of the construction process. The algorithm for data in arbitrary order no longer has that interesting property, but it is more flexible than the one by Dominique Revuz.
Note that it is possible to use the incremental algorithms described
above to build deterministic acyclic finite-state automata with final
transitions . In fact, the algorithms presented in
this chapter are the modified versions of the algorithms for the
DAFSA-FT. Both the vectors of transitions, and the sparse table
representation used by Dominique Revuz et al. can be used with
the DAFSA-FT to obtain smaller automata. The gains depend on the
characteristics of particular data. Table 4.5
provides some examples. The French words were taken from a
morphological lexicon of French from ISSCO,
Geneva. It contains 210284 words. The Polish words come from a lexicon
developed by Prof. Zygmunt Vetulani from Adam Mickiewicz University in
Poznan, Poland. It contains 1012496 words and expressions. The
Polish lexicon is less regular. This may be the reason for bigger
gains with that data. Note that the gains depend on the percentage of
final states in the automaton. It is possible to construct such
deterministic acyclic automata with n states that the corresponding
DAFSA-FT has (n-2)/2+2 state. For large automata of this kind
.
The automaton in figure 2.4 is such an automaton (n=4).
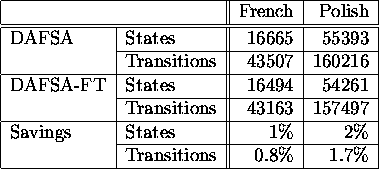
Table 4.5: DAFSA-FT compared with DAFSA dictionaries of French and
Polish words
The same algorithms can be used to construct
transducers . Labels from both levels
can be put one after another (possibly using a filler character where
there is no symbol on any level), and then treated as words for an
automaton, with the alphabet being 
, where 
and 
are the alphabets of the
levels. The transducers constructed in such a way are not
subsequential.
We do not use the representation advocated by Revuz and others (based
on [TY79]). That representation actually
produces smaller dictionaries. This is achieved not by better
placement of states (and their transitions) - this is already optimal
in the vector representation we use, but by eliminating the need to
store the number of transitions parting from a given state. It is also
faster at recognition. However, in applications where one needs to
list or to try all descendants of a state, like in spelling
correction, diacritic restoration, and (partly) morphological
analysis, it is much slower, as one must check all 
possibilities at each state.