The purpose of spelling correction is to verify whether a given text is correct linguistically, i.e. whether it constitutes a sequence of statements that are correct statements of the language the text is written in, and if not, propose means to correct it. The text is correct if all words of the text are:
Possibly incorrect words can be detected by dictionary lookup. A word that is not present in the dictionary may still be a valid word - language is something that changes all the time. However, errors are less likely to be in a dictionary. In the past, statistical techniques were used to detect erroneous words. A program called TYPO ([Pet80]) used frequencies of digrams and trigrams to find possibly incorrect words. Words that contained digrams or trigrams of low frequency were judged to be (possibly) incorrect.
For all incorrect words and expressions, a spelling checker should produce a list of their possible replacements. The replacements are words present in the dictionary that are ``similar'' to the given word in a certain aspect. This similarity can be measured in a number of ways. The most important involve:
Those measures reflect the origins of errors. Errors can be the result of:
Those measures rely solely on the properties of individual words. The
lists of replacements can further be reduced by checking the context
of words. Certain words cannot appear in certain contexts. The
disambiguation can be done using syntactic and semantic analysis,
statistical methods, or machine learning. Although finite-state tools
are used with success on the syntactic level (see
e.g. [RS95], we have not developed our own tools for
that purpose, so these methods are not described here. The reason
those methods were not implemented is that it would involve the
syntactic level, while this work stays on the morphology and lexicon
level (see fig. 1.1). For a description of methods
that do not use finite-state tools, see [CDK
91],
[CDGK92], [CGM93],
[GC92], [HJM82],
[JHMR83], [KS81], and
[Atw87]. The syntactic level (and higher levels) can also
be used to detect words that are correct words of the language and are
present in the lexicon, but that are used in wrong context. These are
most probably incorrect forms of other words.
The edit distance ([Dam64]) between two strings specifies how many basic editing operations are needed to convert one string into the other. The basic editing operations are:
The edit distance between two strings (or words) X and Y of lengths m and n respectively, can be defined as follows ([DC92], [OG94], [Ofl96]):
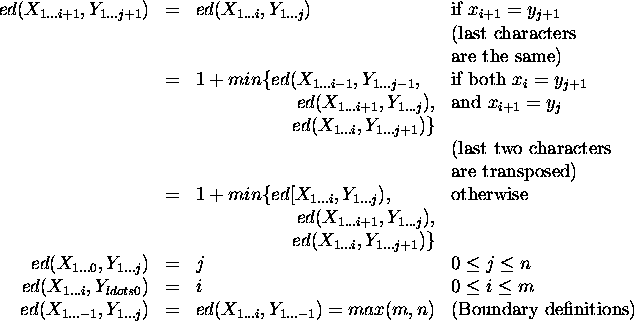
The recursive part of the definition can further be divided into three sections. The first one is obvious: if the last characters are the same, then the edit distance is the same as if we remove them from the ends of the words. For example, ed(aba,bba) = ed(ab,bb) = ed(a,b).
The next section provides a formula that should be applied in case the last letter of the first word is the penultimate letter of the second word, and vice versa. In such situation a transposition of the last two letters of one the words could be one of the transformations that need to be done to obtain the other word, e.g. in case of (ababab,ababba). However, there are other cases that give similar results: deletion (e.g. (aba,abab)), and insertion (e.g. (abab,aba)).
The last section deals with other cases, i.e. when the last letters of the words are neither equal to one another, nor equal to the penultimate letters of the other word. This situation can be the result of one of three operations: replacement of the last letter (e.g. (ababa,ababb)), deletion (e.g. (a,ab)), or insertion (e.g. (ab,a)).
Using the edit distance , we can define the set of
plausible corrections of the word 
as:
where t is the maximum edit distance between the word w and its
correction.
It is possible to attribute different costs to different editing operations. In the following formula, IC is the insertion cost, DC is the deletion cost, CC is the change cost, and TC is the transposition cost. By manipulating the constants, it is possible to favor one type of operation over another.
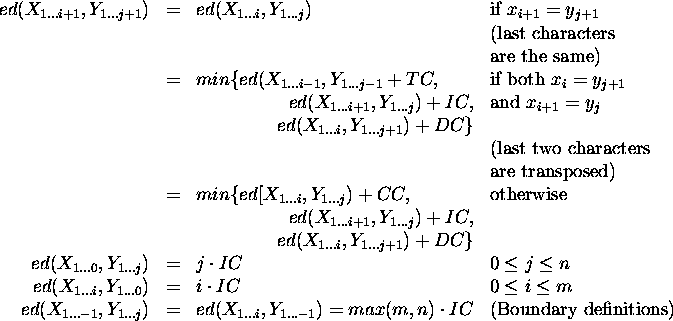
The editing operations that produce typographical errors are reversible, i.e. if a string was obtained by a basic editing operation from a correct word, then the correct word can be obtained by performing a single basic editing operation complementary to that that lead to the error. Insertion and deletion are mutually complementary, and change and transposition are self-complementary.
Because the generation of all strings that lie within the specified edit distance and testing their presence in a lexicon would be very time-inefficient, special techniques were used in the past to limit the number of candidates for corrections. Joseph Pollock and Antonio Zamora ([PZ84]) used a skeleton key and an omission key to index all words in a dictionary that could be corrections of a given incorrect string. The words with the same value of the key as the incorrect string were then tested whether they lied within the given edit distance from the incorrect string. The skeleton key contained the first letter of the incorrect string, unique consonants in order of occurrence, and the unique vowels in order of occurrence.
The omission key was used to find corrections that were not handled by the skeleton key. It was constructed by sorting the unique consonants of the incorrect string in the following order: KQXZVWYBFMGPDHCLNTSR, and then appending the unique vowels in their original order. The order of consonants was established empirically from the frequencies of omissions of those letters from words in corpora.
The pioneering work on spelling correction with finite-state automata was done by Kemal Oflazer ([OG94] and [Ofl96]. We present here his approach along with our modifications for the Polish language.
To find all corrections of the given (erroneous) word, we need to find all paths from the start state to one of the final states, so that when labels on the transitions along a path are concatenated, the resulting string is within a given edit distance threshold t of the erroneous word. As searching needs to be fast, one cannot search the whole automaton. As soon as it becomes clear that the current path does not lead to a solution, we should abandon it. To detect such cases, a notion of cut-off edit distance was introduced ([DC92], [OG94], [Ofl96]). The cut-off edit distance is the minimum edit distance between an initial substring of the incorrect word, and any initial substring of the candidate (correct) word. For the edit distance t, the cut-off edit distance cuted(X,Y) of the string X of length m, and the partial candidate word Y of length n is defined as follows:
The range of lengths of the substrings of X checked is from n - t to n + t, except close to word boundaries. If n - t is less than one, one cannot take a null string, and if n + t is more than the length of X, one cannot append additional characters at the end of X. The depth-first search in the automaton with the use of the cut-off edit distance gives the algorithm ([Ofl96]) given in fig. 6.1.
Figure 6.1: Spelling correction with finite-state automata
Note that it is possible to use automata that store words with
annotations, such as those used in the morphological analysis, with
the algorithms in fig. 6.1 by substituting the test
for t 
for a test on the presence of a transition labeled with
the annotation separator . A dynamic
programming technique can be used to reuse computed values of the edit
distance so that the speed of the algorithms can be improved
([DC92]). Closer examination of the formula for computing the
edit distance shows that the value of
depends on
,
,
, and
. The values of ed can be put
into a matrix H, so that is in
H(i,j). Looking at the algorithm from fig. 6.1,
we can see that before we move to the row j, the values from the row
j-1 are already computed. They stay the same for all transitions
tried in the loop. So we do not need to recompute H(i-2,j-2),
H(i-1,j-1), H(i,j-1). We do need to recompute H(i-1,j). As the
algorithm for computing the cut-off edit
distance proceeds from the rows with smaller indices to those with
bigger ones, the value of H(i-1,j) is always computed before it is
needed in the calculation of H(i,j).
In many languages, one can find words that have different spelling, but that are pronounced either identically, or in a similar way. In Polish, for example, the pairs ó - u and ż - rz have identical pronunciation, and although there are native Polish speakers that distinguish between h (voiced), and ch (not voiced), most Polish speakers pronounce both as ch. As the number of speakers that cannot write properly grows, new types of errors emerge, e.g. ą - on, ą - om, ę - en, and ę - em. The pairs ó - u and h - ch can be treated as typographical errors. However, the pair ż - rz, and the new pairs involving nasal vowels cannot. Finding the words that are pronounced in a similar manner to a given word is usually done with transducers . One transducer level contains the inflected forms, the other one - symbols that represent their pronunciation. The search for candidates for correct forms is done on the pronunciation level, possibly using the edit distance . For languages with highly regular pronunciation (such as Polish), one can do away with automata-acceptors. A solution that takes into account the possibility of replacing a pair of characters with a single character and vice versa is given in fig. 6.2. Note that from the four transformations that produce errors, only one - change is affected. This is because it highly unlikely that someone would accidentally drop or insert two consecutive letters, or would move one letters by two positions. This algorithm is sufficient for Polish. A more elegant and general solution could involve weighted transducers and the local extension algorithm ([RS95], [Moh97]).
Figure 6.2: Spelling correction with finite-state automata with modifications
Application of morphological analysis for correction of lexical errors was proposed in a number of papers, e.g. [CGM93], [CDGK92]. The method requires the following steps:
, the construction of a finite-state
automaton used in it is discussed in chapter 5,
page , and the data for it is discussed in
section 3.3, page . Our
analysis is flectional, so it will not correct errors such as e.g.
upartość that could be an incorrect nominalization of
uparty, while the proper nominalization is upór. It will,
however, detect errors such as e.g. piesa, recognizing that
(among possibly other candidates) the lexeme could be pies, and
the categories should be noun, animal, single, genitive. The
morphological generation with input data being the lexeme and the
categories obtained in the previous step would yield psa. The
morphological generation (analogous to morphological analysis) is
described in section 6.3.1,
page . Note that if the lexeme (or root) is not
present in the lexicon, or if no inflected forms of the given
categories can be found for it, no candidates will be
generated.